Irrational numbers are in fact produced from infinite continued fractions. For example:
The value of a number can be approximated to different accuracies by truncating the continued fraction at different poinst.
Determining the continued fraction for an irrational number is also very interesting and I might cover it in a later post. In this post, I am going to prove the irrationality of some numbers such as √2 and π.
Irrationality of √2:
This is proof by contradiction. Let’s assume there is a simplified fraction a/b which is equal to √2.
a/b=√2
a=b√2
a^2=2b^2
∴a^2 | 2
∴a|2 since a∈Z
Since a is even, b cannot be even (since a/b is a simplified fraction).
Since a is even, there should be an integer k for which a=2k.
(2k)^2=2b^2
4k^2=2b^2
b^2=2k^2
∴b^2 |2
∴b|2 since b ∈Z
But b cannot be even. Since a and b are both even, a/b is not a simplified fraction. Therefore, by proof by contradiction, √2 is irrational. Specifically, this is called proof by infinite descent.
Irrationality of π:
This proof is much more difficult and interesting. We are again going to use proof by contradiction. Since this proof involves a lot of exponents, derivatives, and integrals, I have written the proof in Microsoft Word and I am going to upload it here as images.

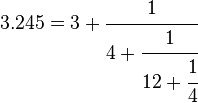





this is some really good stuff that good could easily bake my noodle(brain) now u see wy i call u professor. its stephen. keep it up, u might jus gain alot of viewers and followers and soon everyone will know and then it will go public and even get u faame..but i know u dont need that so we'll stick with it being a hobbby. am i right or left or right or wrong!!! your friend stephen. love it..
ReplyDeletelol thanks Stephen.
ReplyDelete